
선형 검색과 이진 검색
# 알고리즘
어떤 과제를 완수하는 명령어의 집합을 의미한다.
# 정렬된 배열에서의 검색
값이 순서대로 배치된 배열을 정렬된 배열이라고 한다. 정렬된 배열은 일반적인 배열보다 검색이 유리하다. [50, 30, 10, 20, 40] 라는 일반적인(정렬되지 않은) 배열에서 25라는 값을 찾는다고 치자. 이 상황에서는 배열의 처음부터 끝까지 검색을 해야 한다. 그러나 [10, 20, 30, 40, 50]이라는 정렬된 배열에서는 30에 도달했을 때 검색을 멈출 수 있다. 어차피 30뒤에는 30보다 큰 숫자밖에 없기 때문이다. 이렇게 정렬된 배열은 검색 단계를 줄일 수 있다는 장점이 있다.
위에서 사용한 검색 방법은 선형 검색(Linear Search)이다. 그러나 검색 알고리즘에는 선형 검색만 있는 것이 아니다. 바로 다음에 설명할 이진 검색(Binary Search)은 선형 검색보다 훨씬 효율적이고 빠르다.
# 이진 검색
친구가 1부터 100사이의 숫자 중 하나를 머릿 속으로 생각하고, 그 숫자가 무엇인지 맞히는 게임을 해보자. 친구에게 어떻게 질문해야 가장 빠르게 숫자를 찾아낼 수 있을까? 숫자가 1이냐, 2냐, 3이냐, ... 처럼 하나하나 질문하는 것보다 더 빠른 방법은 '그 숫자가 50보다 작아?'라고 묻는 것이다. 50보다 큰지 작은지만 알아내도 경우의 수가 반으로 줄어든다. 만약 50보다 작다면, 그 다음 질문은 25보다 작은지 물어보고, 25보다 작다면 12보다 작은지 물어보면 된다. 이렇게 주어진 숫자들 중, 중간 지점을 골라 나머지 반을 제거해가며 값을 알아내는 방법을 이진 검색이라고 한다.
# 선형 검색과 이진 검색
선형 검색과 이진 검색을 비교해보자. 배열의 크기가 작을 때는 큰 차이가 없지만 배열이 커질수록 효율성도 크게 달라진다. 만약 100개의 원소를 갖는 배열에서 선형 검색을 사용한다면 최대 100단계가 필요하지만, 이진 검색을 사용하면 7단계만에 검색을 끝낼 수 있다. 200개의 원소를 갖는 배열에서 선형 검색은 200단계, 이진 검색은 8단계만에 검색이 끝난다. 즉, 이진 검색은 배열의 크기가 2배로 늘어나도 실행 단계는 단 한 단계만 늘어날 뿐이다.
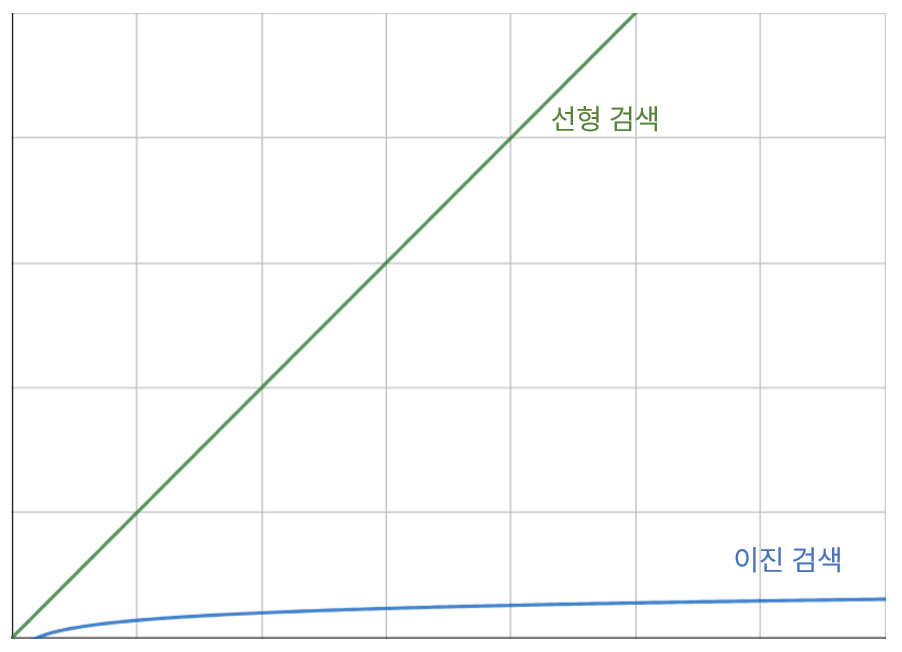
이를 그래프로 나타내면 위와 같다. 데이터가 많아질수록 선형 검색의 검색 단계는 원소 수만큼 늘어나지만, 이진 검색은 조금씩 늘어난다. 즉, 정렬된 배열에서는 이진 검색을 이용하면 훨씬 빠르게 검색을 수행할 수 있다.
# 무조건 정렬된 배열이 좋은가
배열이 정렬되어 있으면 이진 검색을 이용할 수 있어서 검색이 매우 빨라진다. 그렇다면 무조건 배열은 정렬되어 있는 것이 좋은가? 그렇지 않다. 코드의 목적에 따라 다르다. 정렬된 배열은 검색에는 매우 유리하지만 원소 삽입은 느리다. 정렬된 배열에서 삽입을 하기 위해서는 우선 검색 과정을 거치기 때문이다. 삽입 전 검색을 해서 삽입할 위치를 찾아내고 그 이후에 삽입을 진행하기 때문에 정렬되지 않은 배열보다 단계가 더 많아진다.
그러니 코드의 목적에 따라 배열의 정렬 여부를 결정해야 한다. 프로그램에서 삽입이 더 자주 일어나는지 혹은 검색이 더 자주 일어나는지를 명확히 알고 적합한 방식을 선택해야 한다. 이것이 알고리즘을 배우는 이유이다.
참고 자료
책 '누구나 자료 구조와 알고리즘 개정 2판' 2장
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Stack과 Queue (0) | 2023.10.06 |
|---|---|
| [자료구조] Hash Table (0) | 2023.05.03 |
| [자료구조] 정렬 (0) | 2023.04.02 |
| [자료구조] Big O (0) | 2023.03.24 |
| [자료구조] 배열 (0) | 2023.03.11 |



