
정렬
정렬되지 않은 배열이 주어졌을 때, 어떻게 오름차순으로 정렬할 수 있을까? 알고리즘에서 정렬의 방식은 크게 3가지로 설명할 수 있는데, 바로 버블 정렬, 선택 정렬, 삽입 정렬이다. 각 정렬이 무엇인지 알아보고 Big O를 비교하며 그 의미를 파악해보자.
# 버블 정렬 : 두 개의 아이템 비교
1. 배열의 두 개 아이템을 비교한다. 만약 왼쪽이 오른쪽보다 크다면 순서를 바꾼다.
2. 오른쪽으로 이동하여 다시 두 개의 아이템을 비교한다.
3. 이 동작을 반복한다.
예제 (자료 출처 : https://youtu.be/Bor_CRWEIXo)
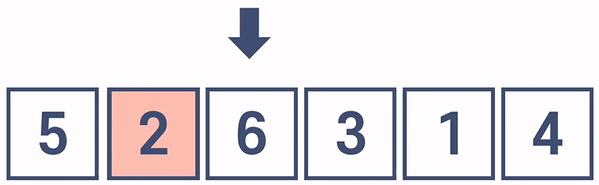
1. 5와 2를 비교한다. 5가 2보다 크기 때문에, 순서를 바꾼다.

2. 5와 6을 비교한다. 6은 5보다 작기 때문에, 순서를 바꾸지 않고 다음으로 넘어간다.

3. 첫 번째 싸이클을 돌면 다음과 같은 순서가 된다. 총 N-1번의 비교를 하였다.

이렇게 하나하나씩 비교하여 순서대로 정렬을 완성하면, 총 몇 번의 비교를 하게 될까? 첫 번째 싸이클에서는 N-1번의 비교를 했으니 두 번째 싸이클에서는 N-2번의 비교를 하게 될 것이다. (가장 마지막 두 개의 아이템을 비교할 필요가 없어지기 때문이다.) 세 번째 싸이클에서는 N-3번의 비교를 하고, 그럼 총 (N-1) + (N-2) + (N-3) + ... + 1번의 비교를 하게 된다.
각 아이템을 비교하고 난 후, 만약 앞의 숫자가 더 크다면 숫자의 위치를 교환한다. 그렇다면 총 몇 번의 교환을 하게 될까? 최악의 시나리오에서는 비교가 일어날 때마다 교환을 하게 된다. 예를 들어 원소가 5개인 배열에서, 최악의 경우에 비교 10번, 교환 10번으로 총 20번의 단계가 필요하다. 만약 원소가 10개라면? 최악의 경우 비교 45번, 교환 45번을 하게 되어 총 90번의 단계가 요구될 수 있다.
버블 정렬은 원소 수 N이 증가할 때마다 단계 수는 N^2로 증가한다. 즉, 버블 정렬의 시간 복잡도는 O(N^2)이다.
# 선택 정렬 : 가장 작은 숫자의 index 기억
1. 배열을 순서대로 확인하며, 가장 작은 숫자의 index를 기억한다.
2. 원소의 끝까지 확인한 뒤, 기억해두었던 index의 원소와 첫 번째 원소의 위치를 바꾼다.
3. 이 동작을 반복한다.
예제
1. 현재 가장 작은 숫자는 5이다. index에 0을 저장한다.

2. 현재 가장 작은 숫자는 2이다. index에 1을 저장한다.

3. 여전히 가장 작은 숫자는 2이다. index에는 1이 저장되어 있다.
4. 원소의 끝까지 비교를 마친 결과, 가장 작은 숫자는 1이다. index에는 4가 저장된다.

5. 첫 번째 원소와 index 4의 원소의 위치를 바꾼다. 첫 번째 싸이클이 종료되었다.

이렇게 하나하나씩 비교하여 순서대로 모든 싸이클이 끝나면, 총 몇 번의 비교를 하게 될까? 버블 정렬과 마찬가지로 총 (N-1) + (N-2) + (N-3) + ... + 1번의 비교를 하게 된다. 그러나, 교환은 한 싸이클 당 1번 발생하거나, 혹은 발생하지 않는다. 즉, 교환은 최악의 시나리오에서도 N-1번만 일어난다. 원소가 5개인 경우, 최대 10번의 비교와 4번의 교환이 발생하여 총 14단계가 요구된다. 원소가 10개라면 최대 45번의 비교와 9번의 교환이 발생하여 총 54단계가 요구된다.
버블 정렬과 비교했을 때, 선택 정렬은 확실히 버블 정렬에 비해 단계가 짧다. 하지만 선택 정렬의 시간 복잡도는 버블 정렬과 동일하게 O(N^2)이다. 어떻게 된 것일까? 바로, 빅 오 표기법에서는 상수가 무시되기 때문이다. 선택 정렬의 시간 복잡도는 N^2 / 2이지만, 빅 오 표기법에서는 1/2라는 상수를 무시하고 N^2라고 표기한다. 즉, 빅 오 표기법에서는 N^2와 N^2 / 2를 같은 것으로 표기한다. 그렇다면 빅 오 표기법은 쓸모가 없는 것일까? 그렇지 않다. 삽입 정렬까지 살펴보고 빅 오 표기법을 다시 살펴보도록 하자.
# 삽입 정렬 : 삭제, 비교, 시프트, 삽입
1. index 1부터 시작하여, 선택한 아이템(A)과 왼쪽 아이템(B)을 비교한다
2. A를 임시로 삭제하고 temp_value라는 변수 속에 저장해둔다.*
3. B와 temp_value 속 A를 비교한다. 만약 B가 A보다 크면 B를 오른쪽으로 시프트한다.*
4. temp_value 속 A를 다시 배열에 삽입한다.*
5. 이 동작을 반복한다.
* 쉽게 말해, 2~4단계는 두 숫자를 비교하고 위치를 교환하는 과정이다. 그러나 원소를 임시로 삭제하고 삽입하는 과정으로 교환이 진행된다.
예제
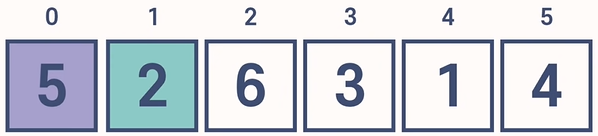
1. 2를 임시로 삭제한 뒤 temp_value에 저장한다. 이때, 2는 5보다 작다. 따라서 5를 오른쪽으로 시프트한다. 그리고 빈 자리에 2를 삽입한다. 즉, 2와 5의 위치가 교환되었다.
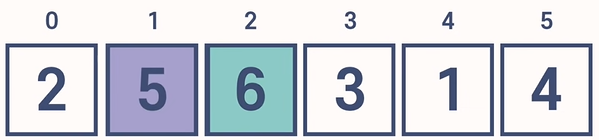
2. 6를 임시로 삭제한 뒤 temp_value에 저장한다. 이때, 6은 5보다 크다. 따라서 시프트를 하지 않고 빈 자리에 다시 6을 삽입한다. 즉, 6은 원래 자신이 있던 자리에 다시 삽입되었고 위치가 변하지 않았다.
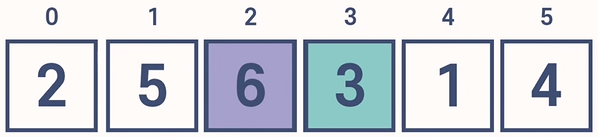
3. 3을 임시로 삭제한 뒤 temp_value에 저장한다. 이때, 3는 6보다 작다. 따라서 6를 오른쪽으로 시프트한다. 그리고 빈 자리에 3를 삽입한다. 즉, 3와 6의 위치가 교환되었다.
4. 3을 임시로 삭제한 뒤 temp_value에 저장한다. 이때, 3는 5보다 작다. 따라서 5를 오른쪽으로 시프트한다. 그리고 빈 자리에 3를 삽입한다. 즉, 3와 5의 위치가 교환되었다.
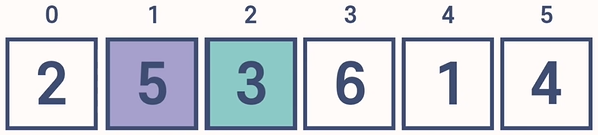
5. 3를 임시로 삭제한 뒤 temp_value에 저장한다. 이때, 3은 2보다 크다. 따라서 시프트를 하지 않고 빈 자리에 다시 3을 삽입한다. 즉, 3은 원래 자신이 있던 자리에 다시 삽입되었고 위치가 변하지 않았다. 첫 번째 사이클이 종료되었다.
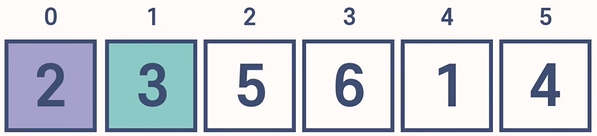
6. 앞서 index 3까지 비교를 했었기 때문에(3단계), 두 번째 싸이클은 index 4부터 시작하여 다시 비교를 시작한다.
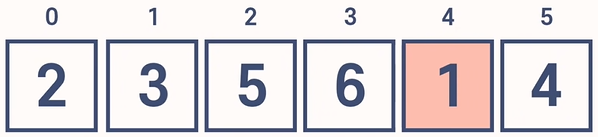
이렇게 삭제, 비교, 시프트, 삽입의 과정을 거쳐 정렬을 완성하면, 총 몇 번의 단계가 필요할까? 비교와 시프트는 합쳐서 최대 N^2로 표현되고, 삭제와 삽입은 최대 N-1으로 표현된다. 즉, 삽입 정렬은 N^2 + 2N - 2 단계가 필요하다. 그러나 빅 오 표기법에서는 상수를 무시하고 가장 높은 차수의 N만 고려하기 때문에, 삽입 정렬의 시간 복잡도는 O(N^2)이다.
버블 정렬보다 선택 정렬이 더 효율적이고, 선택 정렬보다 삽입 정렬이 더 효율적이지만, 3가지 방법 모두 시간 복잡도는 동일하게 표기된다. 빅 오 표기법으로는 알고리즘의 효율성을 확인할 수 없는 것일까? 답은, 그렇지 않다.
# Big O의 의미
각 정렬 방식은 분명히 차이가 있지만 빅 오 표기법으로는 동일하게 표기되는데, 그 이유는 빅 오 표기법은 최악의 시나리오를 고려하기 때문이다. 그러나 우리는 평균 시나리오를 살펴봐야 한다. 통계적으로 평균 시나리오가 가장 자주 발생하기 때문에, 평균적인 관점에서 정렬을 다시 살펴볼 필요가 있다. 선택 정렬과 삽입 정렬을 비교해보자.
| 최선의 시나리오 | 평균 시나리오 | 최악의 시나리오 | |
| 선택 정렬 | N^2 / 2 | N^2 / 2 | N^2 / 2 |
| 삽입 정렬 | N | N^2 / 2 | N^2 |
두 정렬의 시간 복잡도는 경우에 따라 달라진다. 거의 정렬된 데이터를 다룰 때는 삽입 정렬을 사용하는 것이 더 효율적이지만, 데이터의 대부분이 역순으로 정렬되어 있다면 선택 정렬이 더 빠르다. 평균적인 경우 두 정렬은 비슷하게 수행된다. 이처럼 빅 오 표기법을 다룰 때 최선, 평균, 최악의 시나리오를 구분하는 능력을 갖추어야 한다.
참고 자료
책 '누구나 자료 구조와 알고리즘 개정2판' 4, 5, 6장
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Stack과 Queue (0) | 2023.10.06 |
|---|---|
| [자료구조] Hash Table (0) | 2023.05.03 |
| [자료구조] Big O (0) | 2023.03.24 |
| [자료구조] 선형 검색과 이진 검색 (0) | 2023.03.20 |
| [자료구조] 배열 (0) | 2023.03.11 |



