
Big O
# 빅 오(Big O) 표기법
알고리즘의 속도는 실제 시간으로 계산하지 않는다. 시간 복잡도라는 개념으로 판단한다. 하나의 과정을 수행하기 위해 총 몇 가지의 단계를 거치는지를 따지는 것이 곧 빠른 알고리즘 / 느린 알고리즘을 판단하는 기준이 된다. 앞서 배열과 검색을 공부하며 N개의 원소가 있는 배열에서 선형 검색을 하면 총 N단계가 걸린다, 라는 표현을 자주 사용하였다. 그러나 이 표현은 상당히 길고 장황하다. 그래서 보다 명료하게 시간 복잡도를 표현하기 위한 표기법을 사용한다. 바로 빅 오 표기법이다.
# 빅 오 표기법으로 표현한 시간 복잡도
선형 검색은 N개의 원소를 가진 배열에서 최대 N단계를 거친다. 원소가 100개라면 최대 100단계, 200개라면 최대 200단계를 거친다. 이를 빅 오 표기법으로 표현하면 O(N)이 된다. 데이터 원소가 N개일 때 N단계의 알고리즘이 필요하다는 의미이다. 물론 선형 검색은 무조건 N단계가 걸리는 것은 아니다. 경우에 따라 한 단계만에 끝날 수도 있다. 그러나 빅 오 표기법은 최대 몇 단계가 걸리냐를 기준으로 한다. 즉, 최악의 상황에서 몇 단계가 필요한지가 기준이 된다. 선형 검색은 최악의 경우 N단계가 걸리기 때문에, 빅 오 표기법으로 O(N)이 된다.
한 단계만에 끝나는 알고리즘은 어떻게 표현할까? O(1)으로 표현한다. 그렇다면 최대 3단계가 걸리는 알고리즘은 어떻게 표현할까? O(3)이 아니라 O(1)이다. 주어진 배열의 크기가 얼마나 되었든 언제나 3단계만에 끝난다면, 즉 상수로 표현된다면 O(1)이다. N은 단순히 단계의 수가 아니라 함수라고 생각해야 한다. 즉, 배열의 크기가 얼마가 되었든 늘 일정한 단계로 끝나는 알고리즘은 상수 함수로 표현되고, 이를 빅 오 표기법으로 O(1)이라고 한다.
# O(1), O(N), O(logN)
그럼 빅 오 표기법으로 표현할 수 있는 알고리즘의 유형을 더 알아보자. 알고리즘 단계를 상수로 표현할 수 있다면 O(1), 선형 검색처럼 원소 개수만큼 늘어난다면 O(N)이다. 그렇다면 이진 검색은 어떻게 표현할 수 있을까? 이진 검색은 배열의 크기가 두 배로 커져도 단 한 단계만 증가한다. 이를 함수로 표현하면 로그 함수의 형태가 된다. 즉, 빅 오 표기법으로 표현하면 O(logN)이 된다. (이때 로그 함수의 밑은 2이지만 보통 생략해서 적는다.) O(1), O(N) 그리고 O(logN)을 그래프로 표현하면 다음과 같다.
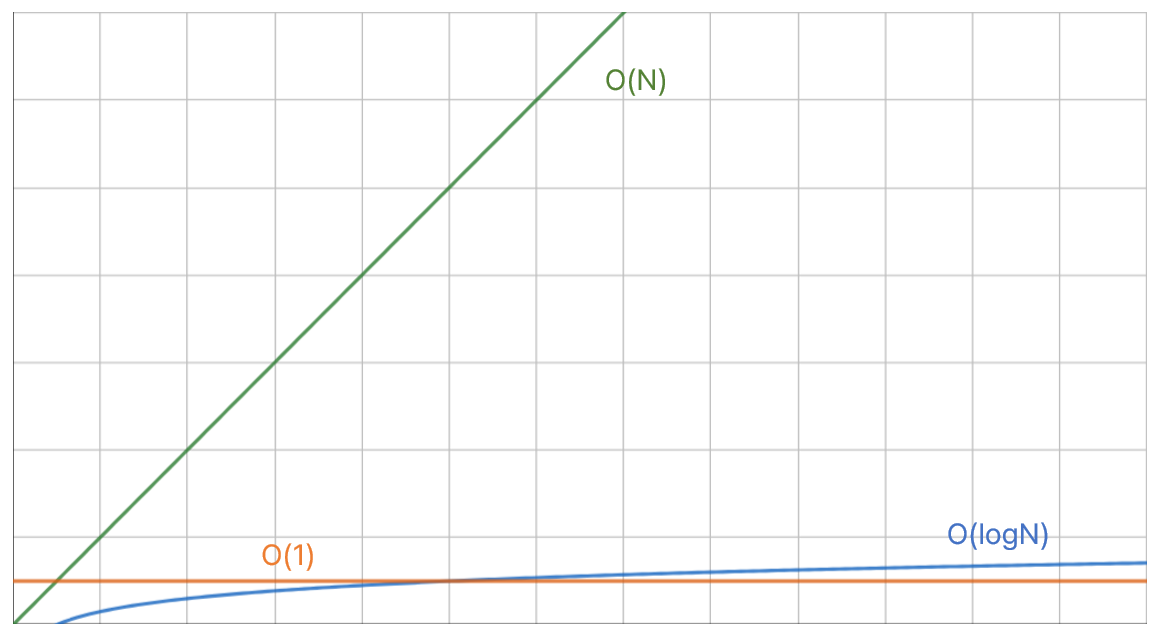
O(1)은 상수 함수이기 때문에 알고리즘 단계 수가 언제나 일정하고, O(N)은 원소의 수만큼 단계가 늘어난다. 그리고 O(logN)은 그 사이에 있다. O(logN)은 원소가 하나가 될 때까지 데이터 원소를 계속해서 반으로 줄여나간다는 의미이다. 즉, O(N)과 비교했을 때 훨씬 더 효율적인 알고리즘이다.
빅 오 표기법으로 시간 복잡도를 바라보면 효율적인 알고리즘이 무엇인지 판단하기 용이하다. 알고리즘에 몇 단계가 걸릴치 분석하는 것이 쉽기 때문에, 알고리즘을 서로 비교할 수 있는 일관된 방법이 되어준다. 따라서 빅 오 표기법을 이용하여 코드의 속도를 더 효율적이고 빠르게 작성하는 방법을 찾아낼 수 있다.
y=x, y=log2(x), y=1이라는 함수 중에서 누가 가장 기울기가 가파를까? 당연히 지수함수가 가장 가파르다 그리고 기울기가 완만할수록 일을 수행하는데 적은 단계가 사용된다는 거니까 더 좋은 알고리즘이 되겠네 하지만 y=상수는 실제로는 구현해내기 어려우니 최대한 로그함수로 표현될 수 있는 알고리즘을 작성하는 것이 좋아보인다 코드의 효율성을 판단할 때 유용할듯😮
이렇게 적으니까 고등학교 미적분 시간으로 돌아온 것 같은데?! ㅋㅋㅋㅋ 지수함수 로그함수.... 괜히 반갑네🤗
참고 자료
책 '누구나 자료 구조와 알고리즘 개정 2판' 3장
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Stack과 Queue (0) | 2023.10.06 |
|---|---|
| [자료구조] Hash Table (0) | 2023.05.03 |
| [자료구조] 정렬 (0) | 2023.04.02 |
| [자료구조] 선형 검색과 이진 검색 (0) | 2023.03.20 |
| [자료구조] 배열 (0) | 2023.03.11 |



